Intersections
Jump to navigation
Jump to search
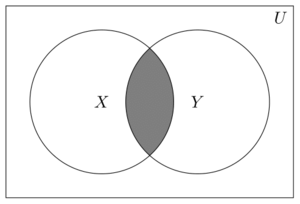
Definition
Let and be subsets of some universal set . The intersection of and , written , is the set of all in which are in both of the sets and .
Symbolically, .
Examples
Example 1
Determine the intersection of the sets and .
Solution. By definition, we wish to find the set of all elements which are in both of the sets. The only such element is . Thus, our solution is .
Example 2
Prove that for any sets and , .
Proof. Let . That is, and . In particular, since we have that .