Implicit Differentiation

Background

So far, you may only have differentiated functions written in the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=f(x)} . But some functions are better described by an equation involving Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} . For example, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{2}+y^{2}=16} describes the graph of a circle with center Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(0,0\right)} and radius 4, and is really the graph of two functions: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\pm\sqrt{16-x^{2}}} .

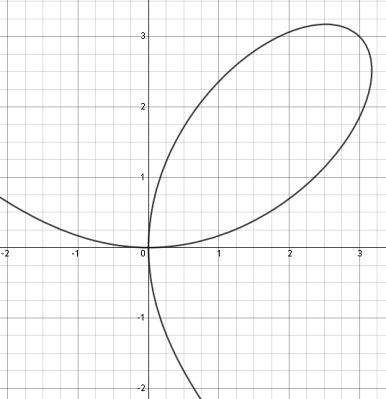
Sometimes, functions described by equations in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} are too hard to solve for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} , for example Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{3}+y^{3}=6xy} . This equation really describes 3 different functions of x, whose graph is the curve:

We want to find derivatives of these functions without having to solve for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} explicitly. We do this by implicit differentiation. The process is to take the derivative of both sides of the given equation with respect to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , and then do some algebra steps to solve for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y'} (or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{dy}{dx}} if you prefer), keeping in mind that $y$ is a function of $x$ throughout the equation.

Warm-up exercises

Given that $y$ is a function of $x$, find the derivative of the following functions with respect to $x$.

1. $y^{2}$

Solution: $2yy'$

Reason: Think $y=f(x)$ and view it as $(f(x))^{2}$ to see that the derivative is $2f(x)f'(x)$ by the chain rule, but write it as $2yy'$.

2. $xy$

Solution: $xy'+y$

Reason: $x$ and $y$ are both functions of $x$, and they are being multiplied together, so the product rule says it's $x\cdot y'+y\cdot 1$.

3. $\cos y$

Solution: $-y'\sin y$

Reason: The function $y$ is inside of the cosine function, so the chain rule gives $(-\sin y)\cdot y'$.

4. ${\sqrt {x+y}}$

Solution: ${\frac {1+y'}{2{\sqrt {x+y}}}}$

Reason: Write it as $(x+y)^{\frac {1}{2}}$, and use the chain rule to get ${\frac {1}{2}}\left(x+y\right)^{-{\frac {1}{2}}}\cdot \left(1+y'\right)$, then simplify.

Exercise 1: Compute y'

Find $y'$ if $\sin y-3x^{2}y=8$.

Note the $\sin y$ term requires the chain rule, the $3x^{2}y$ term needs the product rule, and the derivative of 8 is 0.

We get

${\begin{array}{rcl}\sin y-3x^{2}y&=&8\\\left(\cos y\right)y'-\left(3x^{2}y'+6xy\right)&=&0\quad {\text{(derivative of both sides with respect to x)}}\\\left(\cos y\right)y'-3x^{2}y'&=&6xy\\\left(\cos y-3x^{2}\right)y'&=&6xy\\y'&=&{\dfrac {6xy}{\cos y-3x^{2}}}.\end{array}}$

Exercise 2: Find equation of tangent line

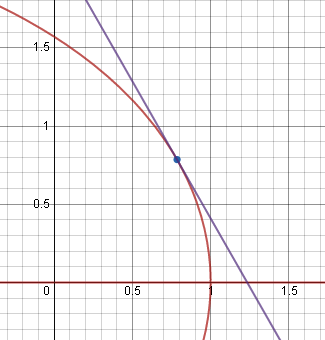
Find the equation of the tangent line to $\tan y={\dfrac {y}{x}}$ at the point $\left({\frac {\pi }{4}},{\frac {\pi }{4}}\right)$.

We first compute $y'$ by implicit differentiation. Note the derivative of the right side requires the quotient rule.

${\begin{array}{rcl}\tan y&=&{\dfrac {y}{x}}\\\left(\sec ^{2}y\right)y'&=&{\dfrac {xy'-y}{x^{2}}}\\x^{2}y'\sec ^{2}y&=&xy'-y\\x^{2}y'\sec ^{2}y-xy'&=&-y\\y'\left(x^{2}\sec ^{2}y-x\right)&=&-y\\y'&=&{\dfrac {-y}{x^{2}\sec ^{2}y-x}}\end{array}}$

At the point $\left({\frac {\pi }{4}},{\frac {\pi }{4}}\right)$, we have Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\frac{\pi}{4}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\frac{\pi}{4}} . Plugging these into our equation for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y'} gives

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} y' & = & \dfrac{-\frac{\pi}{4}}{\left(\frac{\pi}{4}\right)^{2}\sec^{2}\left(\frac{\pi}{4}\right)-\frac{\pi}{4}}\\ \\ & = & \dfrac{-\frac{\pi}{4}}{\frac{\pi^{2}}{16}\cdot2-\frac{\pi}{4}}\\ \\ & = & -\dfrac{\pi}{4}\cdot\dfrac{8}{\pi^{2}-2\pi}\\ \\ & = & \dfrac{2}{2-\pi}. \end{array}}

This means the slope of the tangent line at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{\pi}{4},\frac{\pi}{4}\right)} is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m=\dfrac{2}{2-\pi}} , and a point on this line is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{\pi}{4},\frac{\pi}{4}\right)} . Using the point-slope form of a line, we have

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} y-\frac{\pi}{4} & = & \frac{2}{2-\pi}\left(x-\frac{\pi}{4}\right)\\ \\ y & = & \frac{2}{2-\pi}x-\frac{\pi}{2\left(2-\pi\right)}+\frac{\pi}{4}\\ \\ y & = & \frac{2}{2-\pi}x-\frac{\pi^{2}}{4\left(2-\pi\right)}. \end{array}}

Here's a picture of the curve and its tangent line:

Exercise 3: Compute y' '

Find Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y''} if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ye^{y}=x} .

Use implicit differentiation to find Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y'} first:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} ye^{y} & = & x\\ ye^{y}y'+y'e^{y} & = & 1\\ y'\left(ye^{y}+e^{y}\right) & = & 1\\ y' & = & \dfrac{1}{ye^{y}+e^{y}}\\ & = & \left(ye^{y}+e^{y}\right)^{-1} \end{array}}

Now Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y''} is just the derivative of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(ye^{y}+e^{y}\right)^{-1}} with respect to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} . This will require the chain rule. Notice we already found the derivative of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ye^{y}} to be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ye^{y}y'+y'e^{y}} .

So

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} y'' & = & -1\left(ye^{y}+e^{y}\right)^{-2}\left(ye^{y}y'+y'e^{y}+e^{y}y'\right)\\ \\ & = & \dfrac{-1}{\left(ye^{y}+e^{y}\right)^{2}}\left(ye^{y}y'+2y'e^{y}\right)\\ \\ & = & -\dfrac{y'e^{y}\left(y+2\right)}{\left(e^{y}\right)^{2}\left(y+1\right)^{2}}\\ \\ & = & -\dfrac{y'\left(y+2\right)}{e^{y}\left(y+1\right)^{2}} \end{array}}

But we mustn't leave Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y'} in our final answer. So, plug Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y'=\dfrac{1}{e^{y}\left(y+1\right)}} back in to get

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} y'' & = & -\dfrac{\frac{1}{e^{y}\left(y+1\right)}\left(y+2\right)}{e^{y}\left(y+1\right)^{2}}\\ \\ & = & -\dfrac{y+2}{\left(e^{y}\right)^{2}\left(y+1\right)^{3}} \end{array}}

as our final answer.