Difference between revisions of "Intersections"
Jump to navigation
Jump to search
Scott Roby1 (talk | contribs) |
|||
| Line 1: | Line 1: | ||
== Definition == | == Definition == | ||
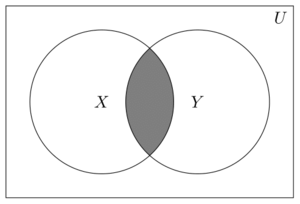
| − | [[File:Intersections.png|thumb|The Venn diagram displays two sets <math>X</math> and <math>Y</math> with the intersection <math>X\cap Y</math> shaded]] | + | [[File:Intersections.png|thumb|The Venn diagram displays two sets <math style="vertical-align: 0px">X</math> and <math style="vertical-align: 0px">Y</math> with the intersection <math style="vertical-align: -1px">X\cap Y</math> shaded]] |
| − | Let <math>X</math> and <math>Y</math> be subsets of some universal set <math>U</math>. The '''''intersection of <math>X</math> and <math>Y</math>''''', written <math>X\cap Y</math>, is the set of all <math>x</math> in <math>U</math> which are in both of the sets <math>X</math> and <math>Y</math>.<br /> | + | Let <math style="vertical-align: 0px">X</math> and <math style="vertical-align: 0px">Y</math> be subsets of some universal set  <math style="vertical-align: 0px">U</math>. The '''''intersection of <math style="vertical-align: 0px">X</math> and <math style="vertical-align: 0px">Y</math>''''', written <math style="vertical-align: -1px">X\cap Y</math>, is the set of all <math style="vertical-align: 0px">x</math> in  <math style="vertical-align: 0px">U</math> which are in both of the sets <math style="vertical-align: 0px">X</math> and <math style="vertical-align: 0px">Y</math>.<br /> |
| − | Symbolically, <math>X\cap Y=\lbrace x\in U : x\in X \text{ and } x\in Y\rbrace</math>. | + | Symbolically, <math style="vertical-align: -5px">X\cap Y=\lbrace x\in U : x\in X \text{ and } x\in Y\rbrace</math>. |
== Examples == | == Examples == | ||
Latest revision as of 11:47, 1 July 2015
Definition
Let and be subsets of some universal set . The intersection of and , written , is the set of all in which are in both of the sets and .
Symbolically, .
Examples
Example 1
Determine the intersection of the sets and .
Solution. By definition, we wish to find the set of all elements which are in both of the sets. The only such element is . Thus, our solution is .
Example 2
Prove that for any sets and , .
Proof. Let . That is, and . In particular, since we have that .