Difference between revisions of "Subsets"
Scott Roby1 (talk | contribs) |
Scott Roby1 (talk | contribs) |
||
| Line 1: | Line 1: | ||
== Definition == | == Definition == | ||
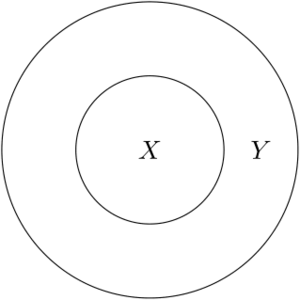
| + | [[File: Subset.png|thumb|An example of a set <math>Y</math> and its subset <math>X</math>]] | ||
Let <math>X</math> and <math>Y</math> be sets. We say that '''''<math>X</math> is a subset of <math>Y</math>''''' if every element of <math>X</math> is also an element of <math>Y</math> , and we write <math>X\subseteq Y</math> or <math>Y\supseteq X</math> . Symbolically, <math>X\subseteq Y</math> means <math>x\in X</math> <math>\Rightarrow</math> <math>x\in Y</math> . | Let <math>X</math> and <math>Y</math> be sets. We say that '''''<math>X</math> is a subset of <math>Y</math>''''' if every element of <math>X</math> is also an element of <math>Y</math> , and we write <math>X\subseteq Y</math> or <math>Y\supseteq X</math> . Symbolically, <math>X\subseteq Y</math> means <math>x\in X</math> <math>\Rightarrow</math> <math>x\in Y</math> . | ||
Latest revision as of 11:44, 29 June 2015
Definition
Let and be sets. We say that is a subset of if every element of is also an element of , and we write or . Symbolically, means .
Two sets and are said to be equal, , if both and . Note that some authors use the symbol in place of the symbol .
Example
Show that the set is a subset of
Solution
We want to show that for any we also have . To do this we will let be an arbitrary element of the set . This means that can be written as for some integer . Now we wish to show that is an element of the set . To do this, we need to show that our satisfies the definition of being an element of ; that is, must look like for some integer . This can be seen by writing and declaring .
Writing Proofs
How to write a proof that : In general, to show we wish to show that if , then . This is done in the following format:
Proof Let . (logical argument), thus . This shows that .
Remark
The logical argument portion often begins by giving the definition of and ends with the definition of .
The following is a write-up of the solution of Example 1 as a formal proof:
Proof Let . That is, there exists some such that . We have . Since , we also have that for an integer , thus . This shows that .