|
|
| Line 123: |
Line 123: |
| | | | |
| | \end{array}</math> | | \end{array}</math> |
| − |
| |
| | | | |
| | This means the slope of the tangent line at <math>\left(0,1\right)</math> is <math style="vertical-align: -13px">m=-\frac{3}{2}</math>, and a point on this line is <math>\left(1,0\right)</math>. Using the point-slope form of a line, we get | | This means the slope of the tangent line at <math>\left(0,1\right)</math> is <math style="vertical-align: -13px">m=-\frac{3}{2}</math>, and a point on this line is <math>\left(1,0\right)</math>. Using the point-slope form of a line, we get |
| Line 133: |
Line 132: |
| | \end{array}</math> | | \end{array}</math> |
| | | | |
| − | Here's a picture of the curve and its tangent line: | + | Here's a picture of the curve and tangent line: |
| | | | |
| − | [[File:Tangent_line.png]] | + | [[File:Tangent_line_and_curve.png|300px]] |
| | | | |
| | == Exercise 3: Compute ''y"'' == | | == Exercise 3: Compute ''y"'' == |
Revision as of 13:31, 21 November 2015
Background
So far, you may only have differentiated functions written in the form  . But some functions are better described by an equation involving
. But some functions are better described by an equation involving  and
and  . For example,
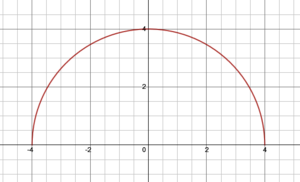
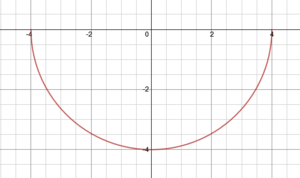
. For example,  describes the graph of a circle with center
describes the graph of a circle with center  and radius 4, and is really the graph of two functions:
and radius 4, and is really the graph of two functions:  , the upper and lower semicircles:
, the upper and lower semicircles:
Sometimes, functions described by equations in  and
and  are too hard to solve for
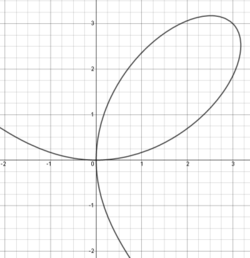
are too hard to solve for  , for example
, for example  . This equation really describes 3 different functions of x, whose graph is the curve:
. This equation really describes 3 different functions of x, whose graph is the curve:
We want to find derivatives of these functions without having to solve for  explicitly. We do this by implicit differentiation. The process is to take the derivative of both sides of the given equation with respect to
explicitly. We do this by implicit differentiation. The process is to take the derivative of both sides of the given equation with respect to  , and then do some algebra steps to solve for
, and then do some algebra steps to solve for  (or
(or  if you prefer), keeping in mind that
if you prefer), keeping in mind that  is a function of
is a function of  throughout the equation.
throughout the equation.
Warm-up exercises
Given that  is a function of
is a function of  , find the derivative of the
following functions with respect to
, find the derivative of the
following functions with respect to  .
.
1) 
| Solution:
|

|
| Reason:
|
Think  and view it as and view it as  to see that the derivative is to see that the derivative is  by the chain rule, but write it as by the chain rule, but write it as  . .
|
2) 
| Solution:
|

|
| Reason:
|
 and and  are both functions of are both functions of  which are being multiplied together, so the product rule says it's which are being multiplied together, so the product rule says it's  . .
|
3) 
| Solution:
|

|
| Reason:
|
The function  is inside of the cosine function, so the chain rule gives is inside of the cosine function, so the chain rule gives  . .
|
4) 
| Solution:
|

|
| Reason:
|
Write it as  , and use the chain rule to get , and use the chain rule to get  , then simplify. , then simplify.
|
Exercise 1: Compute y'
Find  if
if  .
.
Note the  term requires the chain rule, the
term requires the chain rule, the  term needs the product rule, and the derivative of 8 is 0.
term needs the product rule, and the derivative of 8 is 0.
We get

Exercise 2: Find equation of tangent line
Find the equation of the tangent line to  at the point
at the point  .
.
We first compute  by implicit differentiation.
by implicit differentiation.

At the point  , we have
, we have  and
and  . Plugging these into our equation for
. Plugging these into our equation for  gives
gives

This means the slope of the tangent line at  is
is  , and a point on this line is
, and a point on this line is  . Using the point-slope form of a line, we get
. Using the point-slope form of a line, we get

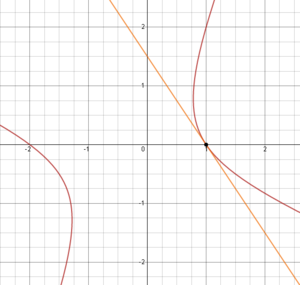
Here's a picture of the curve and tangent line:
Exercise 3: Compute y"
Find  if
if  .
.
Use implicit differentiation to find  first:
first:

Now  is just the derivative of
is just the derivative of  with respect to
with respect to  . This will require the chain rule. Notice we already found the derivative of
. This will require the chain rule. Notice we already found the derivative of  to be
to be  .
.
So

But we mustn't leave  in our final answer. So, plug
in our final answer. So, plug  back in to get
back in to get

as our final answer.