Difference between revisions of "Intersections"
Scott Roby1 (talk | contribs) |
|||
| Line 1: | Line 1: | ||
== Definition == | == Definition == | ||
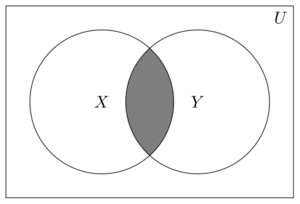
| − | [[File:Intersections.png|thumb|The Venn diagram displays two sets <math>X</math> and <math>Y</math> with the intersection <math>X\cap Y</math> shaded]] | + | [[File:Intersections.png|thumb|The Venn diagram displays two sets <math style="vertical-align: 0px">X</math> and <math style="vertical-align: 0px">Y</math> with the intersection <math style="vertical-align: -1px">X\cap Y</math> shaded]] |
| − | Let <math>X</math> and <math>Y</math> be subsets of some universal set <math>U</math>. The '''''intersection of <math>X</math> and <math>Y</math>''''', written <math>X\cap Y</math>, is the set of all <math>x</math> in <math>U</math> which are in both of the sets <math>X</math> and <math>Y</math>.<br /> | + | Let <math style="vertical-align: 0px">X</math> and <math style="vertical-align: 0px">Y</math> be subsets of some universal set  <math style="vertical-align: 0px">U</math>. The '''''intersection of <math style="vertical-align: 0px">X</math> and <math style="vertical-align: 0px">Y</math>''''', written <math style="vertical-align: -1px">X\cap Y</math>, is the set of all <math style="vertical-align: 0px">x</math> in  <math style="vertical-align: 0px">U</math> which are in both of the sets <math style="vertical-align: 0px">X</math> and <math style="vertical-align: 0px">Y</math>.<br /> |
| − | Symbolically, <math>X\cap Y=\lbrace x\in U : x\in X \text{ and } x\in Y\rbrace</math>. | + | Symbolically, <math style="vertical-align: -5px">X\cap Y=\lbrace x\in U : x\in X \text{ and } x\in Y\rbrace</math>. |
== Examples == | == Examples == | ||
Latest revision as of 11:47, 1 July 2015
Definition
Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y}
be subsets of some universal set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U}
. The intersection of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y}
, written Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\cap Y}
, is the set of all Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U}
which are in both of the sets Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y}
.
Symbolically, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\cap Y=\lbrace x\in U : x\in X \text{ and } x\in Y\rbrace}
.
Examples
Example 1
Determine the intersection of the sets Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X=\lbrace 1,2,5,8 \rbrace} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y=\lbrace 1,3,6,9 \rbrace} .
Solution. By definition, we wish to find the set of all elements which are in both of the sets. The only such element is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} . Thus, our solution is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\cap Y=\lbrace 1 \rbrace} .
Example 2
Prove that for any sets Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\cap Y\subseteq X} .
Proof. Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\in X\cap Y} . That is, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\in X} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\in Y} . In particular, since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\in X} we have that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\cap Y\subseteq X} .