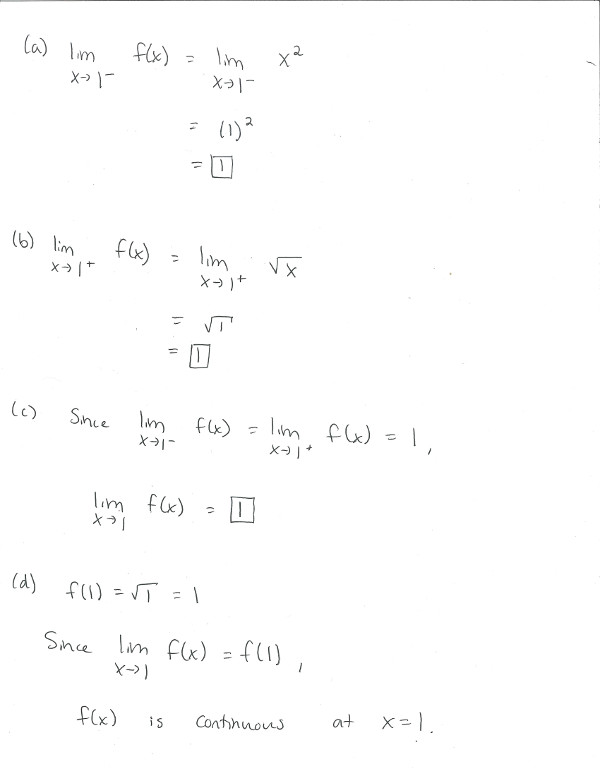Difference between revisions of "009A Sample Midterm 1, Problem 3"
Kayla Murray (talk | contribs) |
Kayla Murray (talk | contribs) |
||
| Line 17: | Line 17: | ||
<hr> | <hr> | ||
| − | [[File:9ASM1P3.jpg|600px]] | + | [[File:9ASM1P3.jpg|600px|thumb|center]] |
| + | |||
[[009A Sample Midterm 1, Problem 3 Detailed Solution|'''<u>Detailed Solution for this Problem</u>''']] | [[009A Sample Midterm 1, Problem 3 Detailed Solution|'''<u>Detailed Solution for this Problem</u>''']] | ||
[[009A_Sample_Midterm_1|'''<u>Return to Sample Exam</u>''']] | [[009A_Sample_Midterm_1|'''<u>Return to Sample Exam</u>''']] | ||
Revision as of 08:28, 5 November 2017
Consider the following function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f:}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = \left\{ \begin{array}{lr} x^2 & \text{if }x < 1\\ \sqrt{x} & \text{if }x \geq 1 \end{array} \right. }
(a) Find Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{x\rightarrow 1^-} f(x).}
(b) Find Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{x\rightarrow 1^+} f(x).}
(c) Find Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{x\rightarrow 1} f(x).}
(d) Is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} continuous at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=1?} Briefly explain.