Difference between revisions of "Implicit Differentiation"

Latest revision as of 17:59, 23 November 2015

Background

So far, you may only have differentiated functions written in the form $y=f(x)$ . But some functions are better described by an equation involving $x$ and $y$ . For example, Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle x^{2}+y^{2}=16} describes the graph of a circle with center Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \left(0,0\right)} and radius 4, and is really the graph of two functions: Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle y=\pm {\sqrt {16-x^{2}}}} , the upper and lower semicircles:

Sometimes, functions described by equations in $x$ and $y$ are too hard to solve for $y$ , for example $x^{3}+y^{3}=6xy$ . This equation really describes 3 different functions of x, whose graph is the curve:

We want to find derivatives of these functions without having to solve for $y$ explicitly. We do this by implicit differentiation. The process is to take the derivative of both sides of the given equation with respect to $x$ , and then do some algebra steps to solve for $y'$ (or ${\dfrac {dy}{dx}}$ if you prefer), keeping in mind that $y$ is a function of $x$ throughout the equation.

Warm-up exercises

Given that $y$ is a function of $x$ , find the derivative of the following functions with respect to $x$ .

1) $y^{2}$

Solution:
$2yy'$

Reason:
Think $y=f(x)$ , and view it as $(f(x))^{2}$ to see that the derivative is $2f(x)\cdot f'(x)$ by the chain rule, but write it as $2yy'$ .

2) Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle xy}

Solution:
$xy'+y$

Reason:
$x$ and $y$ are both functions of $x$ which are being multiplied together, so the product rule says it's $x\cdot y'+y\cdot 1$ .

3) $\cos y$

Solution:
Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle -y'\sin y}

Reason:
The function $y$ is inside of the cosine function, so the chain rule gives $(-\sin y)\cdot y'=-y'\sin y$ .

4) ${\sqrt {x+y}}$

Solution:
${\frac {1+y'}{2{\sqrt {x+y}}}}$

Reason:
Write it as $(x+y)^{\frac {1}{2}}$ , and use the chain rule to get ${\frac {1}{2}}\left(x+y\right)^{-{\frac {1}{2}}}\cdot \left(1+y'\right)$ , then simplify.

Exercise 1: Compute y'

Find $y'$ if $\sin y-3x^{2}y=8$ .

Note the Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \sin y} term requires the chain rule, the $3x^{2}y$ term needs the product rule, and the derivative of 8 is 0.

We get

{\begin{array}{rcl}\sin y-3x^{2}y&=&8\\\left(\cos y\right)y'-\left(3x^{2}y'+6xy\right)&=&0\quad ({\text{derivative of both sides with respect to }}x)\\\left(\cos y\right)y'-3x^{2}y'&=&6xy\\\left(\cos y-3x^{2}\right)y'&=&6xy\\y'&=&{\dfrac {6xy}{\cos y-3x^{2}}}.\end{array}}

Exercise 2: Find equation of tangent line

Find the equation of the tangent line to $x^{2}+2xy-y^{2}+x=2$ at the point Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \left(1,0\right)} .

We first compute $y'$ by implicit differentiation.

{\begin{array}{rcl}x^{2}+2xy-y^{2}+x&=&2\\2x+2xy'+2y-2yy'+1&=&0\\x+xy'+y-yy'+{\frac {1}{2}}&=&0\\xy'-yy'&=&-x-y-{\frac {1}{2}}\\(x-y)y'&=&-(x+y+{\frac {1}{2}})\\y'&=&-{\dfrac {x+y+{\frac {1}{2}}}{x-y}}\end{array}}

At the point Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \left(1,0\right)} , we have $x=1$ and $y=0$ . Plugging these into our equation for $y'$ gives

{\begin{array}{rcl}y'&=&-{\dfrac {1+0+{\frac {1}{2}}}{1-0}}=-{\frac {3}{2}}.\\\end{array}}

This means the slope of the tangent line at Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \left(1,0\right)} is $m=-{\frac {3}{2}}$ , and a point on this line is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(1,0\right)} . Using the point-slope form of a line, we get

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} y-0 & = & -\frac{3}{2}\left(x-1\right)\\ \\ y & = & -\frac{3}{2}x+\frac{3}{2}.\\ \end{array}}

Here's a picture of the curve and tangent line:

Exercise 3: Compute y"

Find Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y''} if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ye^{y}=x} .

Use implicit differentiation to find Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y'} first:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} ye^{y} & = & x\\ ye^{y}y'+y'e^{y} & = & 1\\ y'\left(ye^{y}+e^{y}\right) & = & 1\\ y' & = & \dfrac{1}{ye^{y}+e^{y}}\\ & = & \left(ye^{y}+e^{y}\right)^{-1} \end{array}}

Now Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y''} is just the derivative of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(ye^{y}+e^{y}\right)^{-1}} with respect to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} . This will require the chain rule. Notice we already found the derivative of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ye^{y}} to be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ye^{y}y'+y'e^{y}} .

So

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} y'' & = & -1\left(ye^{y}+e^{y}\right)^{-2}\left(ye^{y}y'+y'e^{y}+e^{y}y'\right)\\ \\ & = & \dfrac{-1}{\left(ye^{y}+e^{y}\right)^{2}}\left(ye^{y}y'+2y'e^{y}\right)\\ \\ & = & -\dfrac{y'e^{y}\left(y+2\right)}{\left(e^{y}\right)^{2}\left(y+1\right)^{2}}\\ \\ & = & -\dfrac{y'\left(y+2\right)}{e^{y}\left(y+1\right)^{2}}\quad (\text{since } e^{y}\neq0). \end{array}}

But we mustn't leave Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y'} in our final answer. So, plug Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y'=\dfrac{1}{e^{y}\left(y+1\right)}} back in to get

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} y'' & = & -\dfrac{\frac{1}{e^{y}\left(y+1\right)}\left(y+2\right)}{e^{y}\left(y+1\right)^{2}}\\ \\ & = & -\dfrac{y+2}{\left(e^{y}\right)^{2}\left(y+1\right)^{3}} \end{array}}

as our final answer.

@@ Line 1: / Line 1: @@
 == Background ==
-So far, you may only have differentiated functions written in the form
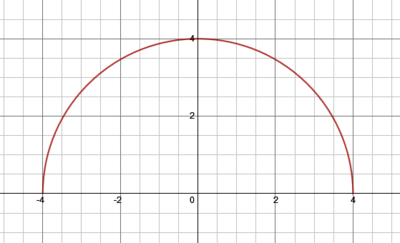
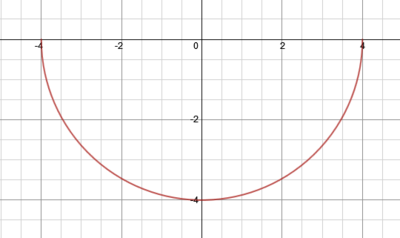
-<math>y=f\left(x\right)</math>. But some functions are better described by an
+So far, you may only have differentiated functions written in the form <math style="vertical-align: -5px">y=f(x)</math>. But some functions are better described by an equation involving <math>x</math> and <math style="vertical-align: -4px">y</math>. For example, <math style="vertical-align: -5px">x^{2}+y^{2}=16</math> describes the graph of a circle with center <math>\left(0,0\right)</math> and radius 4, and is really the graph of two functions: <math style="vertical-align: -5px">y=\pm\sqrt{16-x^{2}}</math>, the upper and lower semicircles:
-equation involving <math>x</math> and <math>y</math>. For example, <math>x^{2}+y^{2}=16</math> describes
-the graph of a circle with center <math>\left(0,0\right)</math> and radius 4,
+{|cellpadding = "10" align="center"
-and is really the graph of two functions: <math>y=\pm\sqrt{16-x^{2}}</math>.
+|[[File:Upper_semicircle.png|400px]]
+|
+|[[File:Lower_semicircle.png|400px]]
+|}
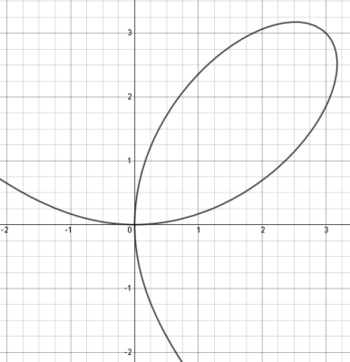
-Sometimes, functions described by equations in <math>x</math> and <math>y</math> are too hard
+Sometimes, functions described by equations in <math style="vertical-align: 0px">x</math> and <math style="vertical-align: -5px">y</math> are too hard to solve for <math style="vertical-align: -5px">y</math>, for example <math style="vertical-align: -5px">x^{3}+y^{3}=6xy</math>. This equation really describes 3 different functions of x, whose graph is the curve:
-to solve for <math>y</math>, for example <math>x^{3}+y^{3}=6xy</math>. This equation really describes 3 different functions of x, whose graph
-is the curve:
+{|cellpadding="25" align="center"
+|[[File:Curve.png|350px]]
+|}
+We want to find derivatives of these functions without having to solve for <math style="vertical-align: -5px">y</math> explicitly. We do this by implicit differentiation. The process is to take the derivative of both sides of the given equation with respect to <math>x</math>, and then do some algebra steps to solve for <math style="vertical-align: -5px">y'</math> (or <math>\dfrac{dy}{dx}</math> if you prefer), keeping in mind that <math style="vertical-align: -4px">y</math> is a function of <math style="vertical-align: 0px">x</math> throughout the equation.
+== Warm-up exercises ==
+Given that <math style="vertical-align: -4px">y</math> is a function of <math style="vertical-align: 0px">x</math>, find the derivative of the
+following functions with respect to <math style="vertical-align: 0px">x</math>.
+'''1)''' &nbsp; <math style="vertical-align: -5px">y^{2}</math>
+{| class = "mw-collapsible mw-collapsed" style = "text-align:left;"
+!Solution: &nbsp;
+|-
+|<math style="vertical-align: -5px">2yy'</math>
+|-
+|}
+{| class = "mw-collapsible mw-collapsed" style = "text-align:left;"
+!Reason: &nbsp;
+|-
+|Think <math style="vertical-align: -5px">y=f(x)</math>, and view it as <math style="vertical-align: -5px">(f(x))^{2}</math> to see that the derivative is <math style="vertical-align: -5px">2f(x)\cdot f'(x)</math> by the chain rule, but write it as <math style="vertical-align: -4px">2yy'</math>.
+|-
+|}
+'''2)''' &nbsp; <math style="vertical-align: -5px">xy</math>
+{| class = "mw-collapsible mw-collapsed" style = "text-align:left;"
+!Solution: &nbsp;
+|-
+|<math style="vertical-align: -5px">xy'+y</math>
+|-
+|}
+{| class = "mw-collapsible mw-collapsed" style = "text-align:left;"
+!Reason: &nbsp;
+|-
+|<math>x</math> and <math style="vertical-align: -5px">y</math> are both functions of <math>x</math> which are being multiplied together, so the product rule says it's <math style="vertical-align: -5px">x\cdot y'+y\cdot1</math>.
+|-
+|}
+'''3)''' &nbsp; <math style="vertical-align: -5px">\cos y</math>
+{| class = "mw-collapsible mw-collapsed" style = "text-align:left;"
+!Solution: &nbsp;
+|-
+|<math style="vertical-align: -5px">-y'\sin y</math>
+|-
+|}
+{| class = "mw-collapsible mw-collapsed" style = "text-align:left;"
+!Reason: &nbsp;
+|-
+|The function <math style="vertical-align: -5px">y</math> is inside of the cosine function, so the chain rule gives <math style="vertical-align: -5px">(-\sin y)\cdot y'=-y'\sin y</math>.
+|-
+|}
+'''4)''' &nbsp; <math style="vertical-align: -5px">\sqrt{x+y}</math>
-We want to find derivatives of these functions without having to solve
+{| class = "mw-collapsible mw-collapsed" style = "text-align:left;"
-for <math>y</math> explicitly. We can do this by implicit differentiation,
+!Solution: &nbsp;
-in which we take the derivative of both sides of our equation with respect
+|-
-to <math>x</math>, and do some algebra steps to solve for <math>y'</math> (or <math>\dfrac{dy}{dx}</math>
+|<math style="vertical-align: -20px">\frac{1+y'}{2\sqrt{x+y}}</math>
-if you prefer), keeping in mind that <math>y</math> is a function of <math>x</math> throughout
+|-
-the equation.
+|}
+{| class = "mw-collapsible mw-collapsed" style = "text-align:left;"
+!Reason: &nbsp;
+|-
+|Write it as <math style="vertical-align: -5px">(x+y)^{\frac{1}{2}}</math>, and use the chain rule to get &nbsp; <math style="vertical-align: -15px">\frac{1}{2}\left(x+y\right)^{-\frac{1}{2}}\cdot\left(1+y'\right)</math>, then simplify.
+|-
+|}
-== Examples ==
+== Exercise 1: Compute ''y''' ==
-. Find <math>y'</math> if <math>\sin y-3x^{2}y=8</math>.
+Find <math style="vertical-align: -4px">y'</math> if <math style="vertical-align: -4px">\sin y-3x^{2}y=8</math>.
-[Think <math>y=f\left(x\right)</math> and momentarily view the equation as <math>\sin f\left(x\right)-3x^{2}f\left(x\right)=8</math>
+Note the <math style="vertical-align: -4px">\sin y</math> term requires the chain rule, the <math style="vertical-align: -4px">3x^{2}y</math>&thinsp; term needs the product rule, and the derivative of 8 is 0.
-to realize that the <math>\sin f\left(x\right)</math> term requires
-the chain rule and the <math>3x^{2}f\left(x\right)</math> term needs the
-product rule when differentiating, while the derivative
-of 8 is just 0.]
-Then we get
+We get
 ::<math>\begin{array}{rcl}
 \sin y-3x^{2}y & = & 8\\
-\left(\cos y\right)\cdot y'-\left(3x^{2}y'+6xy\right) & = & 0\quad \text{(derivative of both sides with respect to x)}\\
+\left(\cos y\right)y'-\left(3x^{2}y'+6xy\right) & = & 0\quad (\text{derivative of both sides with respect to } x)\\
-\left(\cos y\right)\cdot y'-3x^{2}y' & = & 6xy\\
+\left(\cos y\right)y'-3x^{2}y' & = & 6xy\\
 \left(\cos y-3x^{2}\right)y' & = & 6xy\\
-y' & = & \dfrac{6xy}{\cos y-3x^{2}}
+y' & = & \dfrac{6xy}{\cos y-3x^{2}}.
 \end{array}</math>
-. Find the equation of the tangent line to <math>\tan y=\dfrac{y}{x}</math>
+== Exercise 2: Find equation of tangent line ==
-at the point <math>\left(\frac{\pi}{4},\frac{\pi}{4}\right)</math>.
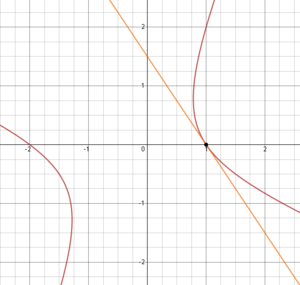
+Find the equation of the tangent line to <math style="vertical-align: -4px">x^{2}+2xy-y^{2}+x=2</math>&thinsp; at the point <math>\left(1,0\right)</math>.
-We first compute <math>y'</math> by implicit differentiation. Note the derivative
+We first compute <math style="vertical-align: -5px">y'</math> by implicit differentiation.
-of the right side requires the quotient rule.
 ::<math>\begin{array}{rcl}
-\tan y & = & \dfrac{y}{x}\\
+x^{2}+2xy-y^{2}+x & = & 2\\
-\left(\sec^{2}y\right)\cdot y' & = & \dfrac{xy'-y}{x^{2}}\\
+x+2xy'+2y-2yy'+1 & = & 0\\
-x^{2}y'\cdot\sec^{2}y & = & xy'-y\\
+x+xy'+y-yy'+\frac{1}{2} & = & 0\\
-x^{2}y'\cdot\sec^{2}y-xy' & = & -y\\
+xy'-yy' & = & -x-y-\frac{1}{2}\\
-y'\left(x^{2}\sec^{2}y-x\right) & = & -y\\
+(x-y)y' & = & -(x+y+\frac{1}{2})\\
-y' & = & \dfrac{-y}{x^{2}\sec^{2}y-x}
+y' & = & -\dfrac{x+y+\frac{1}{2}}{x-y}
 \end{array}</math>
+At the point <math>\left(1,0\right)</math>, we have <math style="vertical-align: -1px">x=1</math> and <math>y=0</math>. Plugging these into our equation for <math style="vertical-align: -5px">y'</math> gives
+::<math>\begin{array}{rcl}
+y' & = & -\dfrac{1+0+\frac{1}{2}}{1-0} = -\frac{3}{2}.\\
+\end{array}</math>
-At the point <math>\left(\frac{\pi}{4},\frac{\pi}{4}\right)</math> we have <math>x=\frac{\pi}{4}</math>
+This means the slope of the tangent line at <math>\left(1,0\right)</math> is <math style="vertical-align: -13px">m=-\frac{3}{2}</math>, and a point on this line is <math>\left(1,0\right)</math>. Using the point-slope form of a line, we get
-and <math>y=\frac{\pi}{4}</math>. Plugging these into our equation for <math>y'</math>
-gives
 ::<math>\begin{array}{rcl}
-y' & = & \dfrac{-\frac{\pi}{4}}{\left(\frac{\pi}{4}\right)^{2}\sec^{2}\left(\frac{\pi}{4}\right)-\frac{\pi}{4}}\\
+y-0 & = & -\frac{3}{2}\left(x-1\right)\\
- & = & \dfrac{-\frac{\pi}{4}}{\frac{\pi^{2}}{16}\cdot2-\frac{\pi}{4}}\\
+\\
- & = & -\dfrac{\pi}{4}\cdot\dfrac{8}{\pi^{2}-2\pi}\\
+y & = & -\frac{3}{2}x+\frac{3}{2}.\\
- & = & \dfrac{2}{2-\pi}
 \end{array}</math>
+Here's a picture of the curve and tangent line:
-This means the slope of the tangent line at <math>\left(\frac{\pi}{4},\frac{\pi}{4}\right)</math>
+[[File:Tangent_line_and_curve.png|300px]]
-is <math>m=\dfrac{2}{2-\pi}</math>, and a point on this line is <math>\left(\frac{\pi}{4},\frac{\pi}{4}\right)</math>.
-Using the point-slope form of a line, we have
-::<math>\begin{array}{rcl}
+== Exercise 3: Compute ''y"'' ==
-y-\frac{\pi}{4} & = & \frac{2}{2-\pi}\left(x-\frac{\pi}{4}\right)\\
-y & = & \frac{2}{2-\pi}x-\frac{\pi}{2\left(2-\pi\right)}+\frac{\pi}{4}\\
-y & = & \frac{2}{2-\pi}x-\frac{\pi^{2}}{4\left(2-\pi\right)}
-\end{array}</math>
-. Find <math>y''</math> if <math>ye^{y}=x</math>.
+Find <math style="vertical-align: -5px">y''</math> if <math>ye^{y}=x</math>.
-Use implicit differentiation to find <math>y'</math> first:
+Use implicit differentiation to find <math style="vertical-align: -5px">y'</math> first:
 ::<math>\begin{array}{rcl}
-y\cdot e^{y} & = & x\\
+ye^{y} & = & x\\
-y\cdot e^{y}y'+y'\cdot e^{y} & = & 1\\
+ye^{y}y'+y'e^{y} & = & 1\\
 y'\left(ye^{y}+e^{y}\right) & = & 1\\
 y' & = & \dfrac{1}{ye^{y}+e^{y}}\\
-  & \textrm{or} & \left(ye^{y}+e^{y}\right)^{-1}
+  & = & \left(ye^{y}+e^{y}\right)^{-1}
 \end{array}</math>
-Now <math>y''</math> is just the derivative of <math>\left(ye^{y}+e^{y}\right)^{-1}</math>
+Now <math style="vertical-align: -5px">y''</math> is just the derivative of <math style="vertical-align: -5px">\left(ye^{y}+e^{y}\right)^{-1}</math> with respect to <math>x</math>. This will require the chain rule. Notice we already found the derivative of <math style="vertical-align: -5px">ye^{y}</math> to be <math style="vertical-align: -5px">ye^{y}y'+y'e^{y}</math>.
-with respect to <math>x</math> (remember <math>y=f\left(x\right)</math>). This will require
-the chain rule. Note that we already found the derivative of <math>ye^{y}</math>
+So
-to be <math>ye^{y}y'+y'e^{y}</math>. So
 ::<math>\begin{array}{rcl}
 y'' & = & -1\left(ye^{y}+e^{y}\right)^{-2}\left(ye^{y}y'+y'e^{y}+e^{y}y'\right)\\
-  & = & \dfrac{-1}{\left(ye^{y}+e^{y}\right)^{2}}\cdot\left(ye^{y}y'+2y'e^{y}\right)\\
+\\
+  & = & \dfrac{-1}{\left(ye^{y}+e^{y}\right)^{2}}\left(ye^{y}y'+2y'e^{y}\right)\\
+\\
   & = & -\dfrac{y'e^{y}\left(y+2\right)}{\left(e^{y}\right)^{2}\left(y+1\right)^{2}}\\
-  & = & -\dfrac{y'\left(y+2\right)}{e^{y}\left(y+1\right)^{2}}
+\\
+  & = & -\dfrac{y'\left(y+2\right)}{e^{y}\left(y+1\right)^{2}}\quad (\text{since } e^{y}\neq0).
 \end{array}</math>
-But we mustn't leave <math>y'</math> in our final answer. So, plug <math>y'=\dfrac{1}{e^{y}\left(y+1\right)}</math>
+But we mustn't leave <math style="vertical-align: -5px">y'</math> in our final answer. So, plug <math>y'=\dfrac{1}{e^{y}\left(y+1\right)}</math>
 back in to get
-<math>\begin{array}{rcl}
+::<math>\begin{array}{rcl}
 y'' & = & -\dfrac{\frac{1}{e^{y}\left(y+1\right)}\left(y+2\right)}{e^{y}\left(y+1\right)^{2}}\\
+\\
   & = & -\dfrac{y+2}{\left(e^{y}\right)^{2}\left(y+1\right)^{3}}
 \end{array}</math>